Los cuadrados mágicos son distribuciones de números en forma de matriz cuadrada tal que las sumas de todas sus filas, columnas y de sus dos diagonales principales es constante. Habitualmente se permite emplear únicamente números naturales consecutivos, lo que a veces se denomina "cuadrado mágico normal".

La generación de cuadrados mágicos es un pasatiempo propio de la matemática recreativa y se pueden encontrar ejemplos de estos en muchos trabajos artísticos, a menudo ligados a la simbología mística.

En este problema implementaremos un algoritmo para generar cuadrados mágicos de orden impar, el denominado algoritmo de De la Loubére. El procedimiento para rellenar una matriz de tamaño ~n\times n~ es el que sigue:

• Se comienza en la casilla central de la primera fila, donde se coloca el número 1.
• Hasta que se rellene la matriz, se repite el siguiente proceso:
  • Se considera una posición hacia arriba (si se está en la primera fila, se cambia a la última) y hacia la derecha (si se está en el borde, se cambia a la primera columna). Si está libre se avanza a dicha casilla. En otro caso, se baja una casilla (si se está en la última fila, se sube a la primera).
  • Se coloca el siguiente natural.

Al término del proceso se habrán colocado los primeros ~n^2~ naturales en una matriz que define un cuadrado mágico.

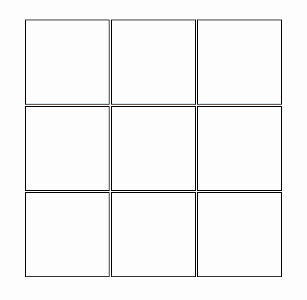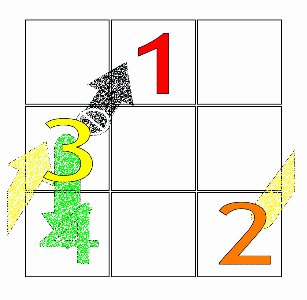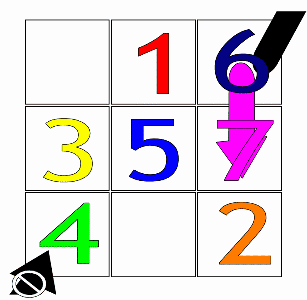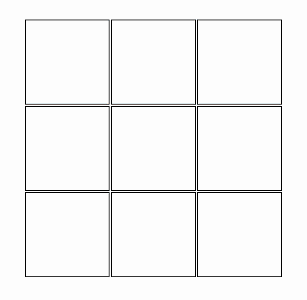
Ejemplo de aplicación del algoritmo para ~n=3~ (imagen enlazada de Wikimedia Commons).

Implementar este algoritmo para matrices cuadradas ~n\times n~ con ~n \leq 31~. Se puede suponer que ~n~ siempre será impar.

Entrada

El valor de ~n~.

Salida

El cuadrado mágico que resulta del algoritmo descrito, escribiendo con tres cifras los enteros (rellenando con espacios si tiene menos), separados por espacios y con un salto de línea entre filas.

Ejemplo de entrada 1

3

Ejemplo de salida 1

  8   1   6
  3   5   7
  4   9   2

Ejemplo de entrada 2

7

Ejemplo de salida 2

 30  39  48   1  10  19  28
 38  47   7   9  18  27  29
 46   6   8  17  26  35  37
  5  14  16  25  34  36  45
 13  15  24  33  42  44   4
 21  23  32  41  43   3  12
 22  31  40  49   2  11  20

Ejemplo de entrada 3

13

Ejemplo de salida 3

 93 108 123 138 153 168   1  16  31  46  61  76  91
107 122 137 152 167  13  15  30  45  60  75  90  92
121 136 151 166  12  14  29  44  59  74  89 104 106
135 150 165  11  26  28  43  58  73  88 103 105 120
149 164  10  25  27  42  57  72  87 102 117 119 134
163   9  24  39  41  56  71  86 101 116 118 133 148
  8  23  38  40  55  70  85 100 115 130 132 147 162
 22  37  52  54  69  84  99 114 129 131 146 161   7
 36  51  53  68  83  98 113 128 143 145 160   6  21
 50  65  67  82  97 112 127 142 144 159   5  20  35
 64  66  81  96 111 126 141 156 158   4  19  34  49
 78  80  95 110 125 140 155 157   3  18  33  48  63
 79  94 109 124 139 154 169   2  17  32  47  62  77